knn近邻算法

Data Science
Data Science
发布日期:   2025-09-30
更新日期:   2025-10-01
文章字数:   2.7k
阅读时长:   9 分
阅读次数:  

什么是k近邻算法：

通俗的例子：根据你的邻居判断你是什么类型，也就是根据你的距离来判断

· 定义

如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数术语某一个类别，则这个样本也属于这个类别

距离度量

1.欧式距离

以上是n维空间点a与b之间的欧式距离

2.曼哈顿距离

在曼哈顿街区从一个十字路口开车到另一个十字路口，驾驶距离显然不是两点间的直线距离。而这个实际距离就是“曼哈顿距离”。也被成为“城市街区距离”

3.切比雪夫距离

国际象棋中，国王可以直行、横行、邪行，所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到(x2,y2)最少需要多少步？这个距离就是切比雪夫距离

4.闵可夫斯基距离

不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述。

p = 1 是曼哈顿距离，2是欧式距离，无穷就是切比雪夫距离

小结

  1. 这些距离都有明显的缺点，下面是例子：
    二维样本 (身高[单位：cm]，体重[单位：kg])，现有三个样本：a(180,50)，b(190,50)，c(180,60)
    a与b的闵氏距离(包括曼哈顿、切比雪夫)等于a与c的闵氏距离，但实际上身高的10cm并不能和体重的10kg划等号
  2. 闵氏距离的缺点：
    • 将各个分量的量纲，也就是“单位相同的看待了”
    • 未考虑各个分量的分布(期望、方差等)可能是不同的

5.标准化欧式距离

思路：既然数据各维分量的分布不一样，那先将各个分量都“标准化”到均值、方差相等。假设样本集X的均值(mean)为m，标准差(standard deviation)为s，X的“标准化变量”表示为：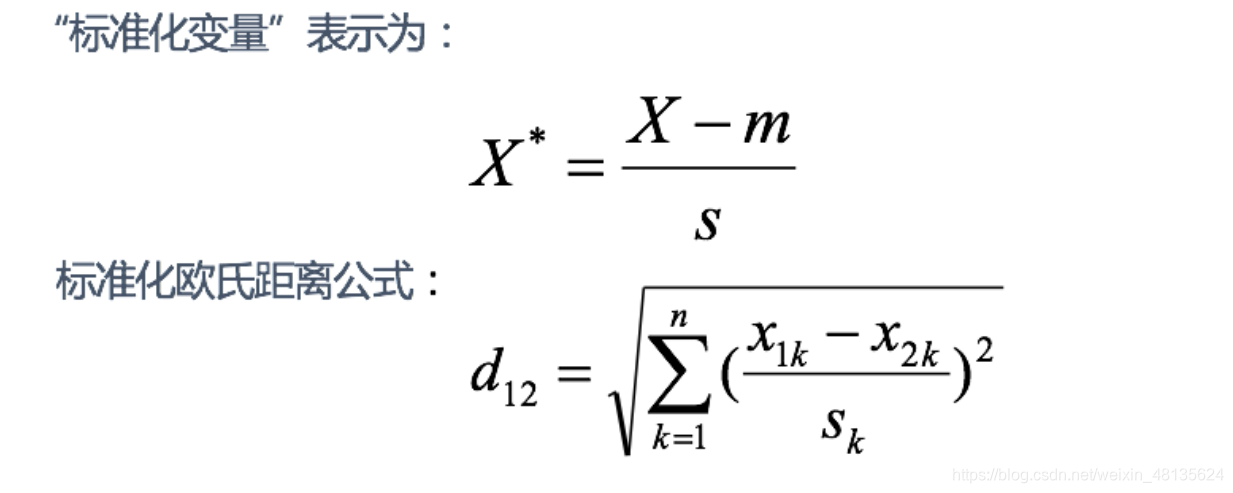

如果将方差的倒数看成一个权重，也可以称之为加权欧式距离

6.余弦距离

几何中，夹角余弦可用来衡量两个向量方向的差异；机器学习中，借用这一概念来衡量样本向量之间的差异。
二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式：

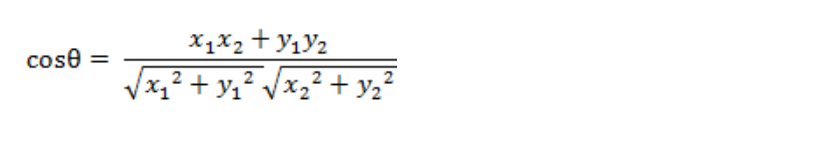两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦为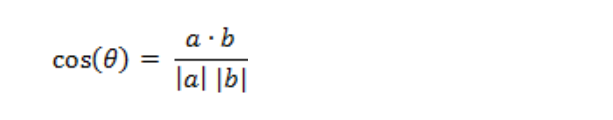： 即：

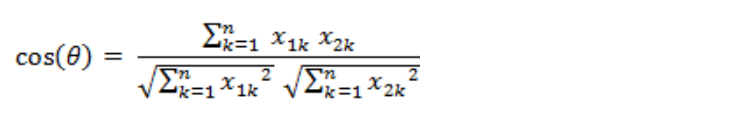
夹角余弦取值范围为[-1,1]。余弦越大表示两个向量的夹角越小，余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值1，当两个向量的方向完全相反余弦取最小值-1。

k值得选择

  • k值过小：容易受到异常点的影响

  • k值过大：受到样本均衡的影响

  • 近似误差：近似误差过小可能出现过拟合的现象，对现有的训练集能有很好的预测，但是对位置的测试样本将会出现较大变差的预测。模型本身不是最接近最佳模型

  • 估计误差：可以理解为测试集的测试误差，关注测试集，估计误差小说明对未知数据的预测能力好，模型本身最接近最佳模型

k值选择问题

  1. 如果选择较小的k值，相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实际较近或相似的训练实例才会对预测结果起作用，与此同时——“学习”的估计误差会增大，简短的说就是：k值减小，整体模型变得复杂，容易发生过拟合
  2. 如果选择较小的k值，相当于用较大的领域中的训练实例进行预测，优点就是减少学习的估计误差，但近似误差增大，输入不相似的巡训练实例也会对预测器起作用，使预测发生错误，且k值得增大意味着模型变得简单
  3. 实际应用中，一般选择较小的k值，，把低纬数据集映射到高纬特征空间

kd数

1.1 什么是kd数

根据knn每次需要预测一个点时，都需要计算训练数据集里每个点到这个点的距离，然后选出距离最近的k个点进行投票，当数据集很大时，则计算成本非常高，

举个例子

一.项目背景——糖尿病数据集

代码区

fold
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
# 第一步：导入必要的库
import pandas as pd   #处理表格数据
import numpy as np    #数值计算
import matplotlib.pyplot as plt  #数据可视化
#以下是机器学习相关工具
#划分训练集和测试集
from sklearn.model_selection import train_test_split
#数据标准化
from sklearn.preprocessing import StandardScaler
#knn分类模型
from sklearn.neighbors import KNeighborsClassifier
#混淆矩阵(用于评估分类模型)
from sklearn.metrics import confusion_matrix
#准确率 也是评估模型
from sklearn.metrics import accuracy_score

# 第二步：加载数据集
df = pd.read_csv('diabetes_dataset.csv')
df.head(5)
df.info()   #查看数据集的基本信息
#以上两步用于了解数据集的初步信息

df.shape  #(行数, 列数)
df.isna().sum()   #查看数据集中是否有缺失值
df.Insulin.sum()   #数据集中的Insulin(胰岛素)列的总和
df.Insulin   #直接查看Insulin列的数据

#以上是针对具体特征的探索，帮你了解该特征的分布或数值范围
#第三步：数据可视化
#绘制数据集的直方图

w = 5
df.hist(bins=10, figsize=(20,15), color='green', alpha=0.6, hatch='X', rwidth=w);
#hist()函数用于绘制直方图，查看每个特征的数值分布(比如血糖主要集中在哪个范围)
#bins参数指定直方图分多少个区间，figsize参数指定图的大小，color参数指定颜色，alpha参数指定透明度，hatch参数指定条形图的形状，rwidth参数指定条形的宽度


#第四步：准备输入特征和标签
X = df.iloc[:, 0:8]  #获取前8列作为输入特征
y = df.iloc[:, 8]  #获取第9列作为标签(是否患有糖尿病)
#第五步：划分训练集和测试集
#训练特征、训练标签、测试特征、测试标签
xtr, xte, ytr, yte = train_test_split(X, y, test_size=0.2, random_state=4)
# random_state=4 用于固定随机数种子，保证结果可以重复
#第六步 ：数据标准化
sc = StandardScaler()   # 初始化标准化工具（将数据转换为均值0、标准差1的分布）
xtr = sc.fit_transform(xtr)  # 对训练数据进行标准化
xte = sc.transform(xte)  # 对测试数据进行标准化
#第七步：训练KNN分类模型
# 创建KNN分类器对象，指定邻居数为11，找11个最近邻居来判断测试样本的类别
# p=2 指定距离度量方式为欧式距离 p=1 为曼哈顿距离

clf = KNeighborsClassifier(n_neighbors=11, p=2, metric='euclidean')

'''
fit_transform(xtr) 会计算训练集的均值和标准差并用于标准化；
但如果对测试集也用 fit_transform，会重新计算测试集的均值和标准差，导致两者 “尺度不同”。
KNN 是基于距离的算法，这种差异会严重影响模型预测效果，导致评估结果失真。
'''
clf.fit(xtr,ytr)
pred = clf.predict(xte)
#第八步：模型预测和评估
print(confusion_matrix(pred, yte))  # 打印混淆矩阵
print(accuracy_score(pred, yte))  ## 打印准确率（(TP+TN)/(总样本数)）

你需要掌握的

1. 数值计算与数据处理库

  • import numpy as np

    NumPy 是 Python 中用于数值计算的核心库，提供了高效的多维数组（ndarray）和大量数学运算函数（如矩阵运算、统计函数等）。在机器学习中，数据通常以数组形式存储和处理，NumPy 是几乎所有数据处理和模型计算的基础。

  • import pandas as pd

    Pandas 是基于 NumPy 的数据处理库，主要用于处理结构化数据（如表格数据）。它提供了 DataFrame 数据结构，方便进行数据清洗、筛选、分组、合并等操作，是读取和预处理 CSV/Excel 等表格数据的常用工具。

2. 可视化库（可选）

  • import matplotlib.pyplot as plt

    Matplotlib 是 Python 中最基础的可视化库，可用于绘制折线图、散点图、直方图、箱线图等。在机器学习中，常用来分析数据分布（如特征与标签的关系）、可视化模型结果（如准确率变化曲线）等，帮助理解数据和模型。

3. KNN 模型与数据处理工具

  • from sklearn.neighbors import KNeighborsClassifier

    这是 scikit-learn（Python 最流行的机器学习库）中的 K 近邻（KNN）分类算法。KNN 是一种简单的监督学习算法，通过计算新样本与训练集中 “最近的 K 个样本” 的类别，来预测新样本的类别，适用于分类任务。

  • from sklearn.model_selection import train_test_split

    用于将数据集划分为训练集和测试集。训练集用于训练模型，测试集用于评估模型在新数据上的表现，避免模型 “记住” 训练数据而泛化能力差（过拟合）。

  • from sklearn.preprocessing import StandardScaler

    用于数据标准化处理。它会将特征值转换为均值为 0、标准差为 1 的分布，消除不同特征量级的影响（例如，“年龄” 和 “收入” 的单位不同），让 KNN 等基于距离的算法更准确。

4. 模型评估指标

  • from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score

    这些是分类任务中常用的模型评估指标：

    • accuracy_score：准确率，正确预测的样本占总样本的比例。
    • precision_score：精确率，预测为 “正类” 的样本中实际为正类的比例（关注预测的准确性）。
    • recall_score：召回率，实际为 “正类” 的样本中被正确预测的比例（关注是否漏检）。
    • f1_score：精确率和召回率的调和平均，综合反映模型性能。

总结

这些工具组合起来，可以完成一个完整的 KNN 分类任务流程：用 Pandas 读取和预处理数据 → 用 StandardScaler 标准化特征 → 用 train_test_split 划分数据集 → 用 KNeighborsClassifier 训练模型 → 用评估指标检验模型效果 → （可选）用 Matplotlib 可视化分析过程或结果。

文章作者: Xxx
文章链接: http://example.com/2025/09/30/knn-jin-lin-suan-fa/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 Xxx !
Data Science
赏
  目录