好的!咱们就完全围绕“下山”这个场景,把梯度下降的核心逻辑、关键步骤和容易踩的坑讲明白,全程不碰复杂公式,只聊“下山时你会怎么操作”。
以爬山为例子
先定个大目标:找到山的“最低谷”
梯度下降的最终目的,是找到“损失函数最小的点”(对应线性回归里“最贴合数据的直线”)。
在下山场景里,这个目标就对应:走到整座山的“最低谷” —— 这里是整座山海拔最低的地方,再也找不到比这更低的位置(就像损失函数再也找不到更小的值)。
咱们就把你当成“要下山找低谷的人”,一步步看梯度下降是怎么帮你实现的。
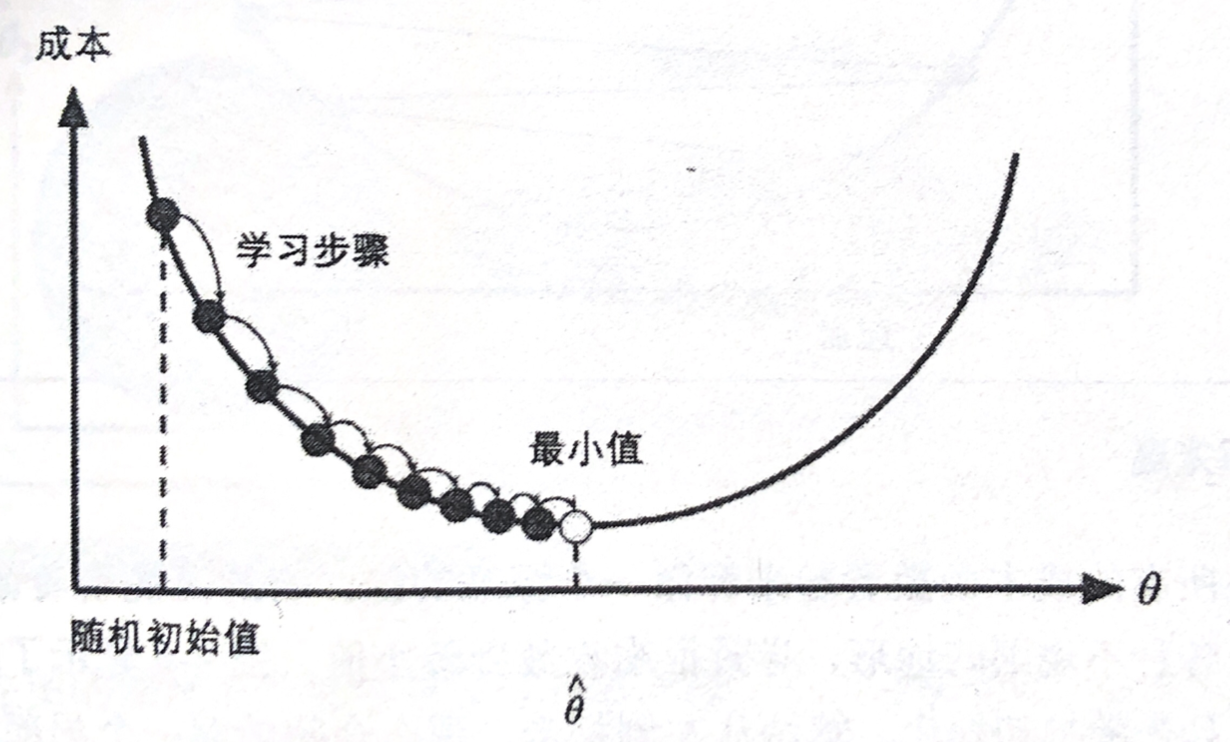
第一步:先随便找个“起点”(对应初始参数w、b)
你不可能凭空出现在山里,总得有个“开始的位置”。
比如:你可能早上出发时,随机站在山的某个半山腰(比如“海拔800米,坐标(东300米,北200米)”)—— 这个“起点位置”,就对应线性回归里我们先“随便猜”的初始参数(比如先假设直线的斜率w=1,截距b=0)。
注意:起点不用“精准”,哪怕站在山顶、山脚边都没关系,梯度下降后续会帮你调整方向。
第二步:搞懂“梯度”:它是你的“下山方向指南”
站在起点后,你第一个问题肯定是:“往哪走一步,能最快往山下走?”
[!NOTE]
这时候“梯度”就派上用场了——它不是一个“距离”,而是一个“方向”,专门告诉你:
“在当前这个位置,往哪个方向走,海拔下降得最快(也就是下山最效率)”。
举个具体例子:
你站在起点(海拔800米),环顾四周后发现:
- 往“正西方”走1步,海拔能从800米降到780米(降20米);
- 往“正南方”走1步,海拔只能降到795米(降5米);
- 往“正东方”走1步,海拔反而升到810米(往山上走了)。
那“梯度”此时就会明确指给你:“往正西方走!这是当前下山最快的方向”—— 而“梯度的反方向”(因为梯度本身指“上山最快的方向”,反方向才是“下山最快”),就是你下一步该走的路。
对应到线性回归里:“梯度”会告诉你“当前的w和b,该往哪个方向调整(比如w变大一点?还是b变小一点?),才能让损失函数降得最快”。
第三步:控制“步长”(对应学习率α):别一步跨太大摔下去
知道往“正西方”走了,但你还要决定:“这一步走多大?是迈小碎步(走1米),还是大跨步(走100米)?”
这个“步长”,就是梯度下降里的“学习率(α)”—— 它决定了你每次调整方向时,“参数变化的幅度”。
这里有两个关键坑,咱们用下山场景直接说透:
坑1:步长太大(学习率α过高)—— 可能“摔下山”或“绕远路”
比如你嫌小碎步太慢,直接迈“100米的大跨步”往正西方走:
- 可能原本前方10米处是个陡坡,你一步跨过去,直接摔进山谷里(对应参数调整幅度过大,损失函数不仅没减小,反而突然变超大);
- 也可能你跨过了“最低谷”,直接走到了对面的半山腰(比如从800米跨到600米,但跳过了500米的低谷,反而到了550米的位置),之后又得往回走,绕了远路。
坑2:步长太小(学习率α过低)—— 下山太慢,永远到不了终点
比如你只敢迈“10厘米的小碎步”:
- 虽然每一步都在往山下走,但走1小时才从800米降到790米,要走到500米的低谷,可能需要几天几夜(对应模型训练时,损失函数下降极慢,训练1000轮还没找到最小值,效率太低)。
正确的做法:步长“适中”
就像下山时,你会根据路面情况调整步长:平缓的地方迈大一点,陡峭的地方迈小一点—— 学习率也需要“适中”,既能保证快速下山,又不会摔下去或绕路(实际训练中,一般会选0.01、0.001这样的小值,避免踩坑)。
第四步:重复“看方向→走一步”,直到走到“低谷”
找到方向、定好步长后,你要做的就是“重复操作”:
- 站在当前位置(比如800米→780米),再看梯度指的新方向(比如这次梯度让你往“西南方”走);
- 按固定步长走一步(比如再走10米,到765米);
- 再站在765米的位置,看新方向→走一步→……
这个过程会一直重复,直到出现一个关键信号:“你走一步后,海拔几乎没变”。
比如:你从500.1米的位置,按步长走一步,到了500.0001米—— 此时你就知道:“到低谷了!再走也降不下去了”,于是停下来。
对应到线性回归里:就是“调整一次w和b后,损失函数的值几乎不变”—— 这时候就说明,我们找到了“最贴合数据的直线”,可以停止训练了。
最后总结:下山=梯度下降的完整逻辑
把整个过程串起来,你会发现“下山”和“梯度下降”完全是一回事:
| 下山场景(你要做的事) | 梯度下降(模型要做的事) | 核心对应关系 |
|---|---|---|
| 目标:走到山的最低谷 | 目标:找到损失函数最小值 | 最终目的一致 |
| 起点:随机站在山腰某位置 | 起点:随机设定初始w、b | 初始状态一致 |
| 方向:看梯度指“下山最快的方向” | 方向:计算梯度,确定w、b的调整方向 | 决策依据一致 |
| 步长:按适中的步伐走一步 | 步长:按学习率α调整w、b的幅度 | 执行幅度一致 |
| 停止:走一步海拔几乎不变 | 停止:损失函数几乎不变 | 终止条件一致 |
这样是不是就完全懂了?梯度下降本质就是“让模型像人下山一样,一步步找到最优解”—— 没有复杂的数学,就是“看方向、走小步、重复到终点”的过程。
接下来用一个简单的函数举个例子
我们选一个超简单的单变量函数:$f(x) = x^2$(图像是开口向上的“抛物线”,最低点在$x=0$处,此时$f(x)=0$)。
第一步:确定“起点”(对应初始参数$x_0$)
假设你一开始随机站在“$x=3$”的位置(也就是山的“右边3米处”),此时你的海拔高度是$f(3)=3^2=9$米(相当于初始损失值)。
这一步对应梯度下降的“初始参数设定”——不用纠结起点对不对,哪怕选$x=5$、$x=-4$都没关系,后续会调整。
第二步:找“下山方向”(计算梯度,确定$x$的调整方向)
站在$x=3$(海拔9米),你要先搞清楚:往左边走,还是往右边走,海拔会下降?
这就是“梯度”要解决的问题。对$f(x)=x^2$来说,它的“梯度”(数学上是导数$f’(x)$)很简单:$f’(x)=2x$
[!NOTE]
你只需要知道:梯度能告诉你当前位置,$x$往哪个方向变,$f(x)$会降得最快
我们计算当前起点$x=3$的梯度:
$f’(3)=2×3=6$(结果是“正数”)
梯度的含义:
- 若梯度为正数:说明“$x$越大,$f(x)$(海拔)越高”—— 那反过来,要让海拔下降,就得让$x$变小(往左边走)。
- 若梯度为负数(比如你站在$x=-2$,梯度$f’(-2)=-4$):说明“$x$越小,$f(x)$越高”—— 要让海拔下降,就得让$x$变大(往右边走)
所以现在,你明确了“下山方向”:往左边走(让$x$从3变小)
第三步:定“步长”(学习率$\alpha$),走第一步
知道往左边走了,接下来要确定“一步走多大”—— 这就是“步长”(对应梯度下降的学习率$\alpha$)。我们选一个简单的步长:$\alpha=0.1$(意思是“每次调整$x$时,变化幅度是梯度的0.1倍”)。
梯度下降中,$x$的更新公式(用下山话翻译):
新位置 = 当前位置 - 步长 × 梯度
(减号是因为要往“梯度的反方向”走,也就是下山方向)
我们计算第一步后的新位置$x_1$:
$x_1 = x_0 - \alpha×f’(x_0) = 3 - 0.1×6 = 3 - 0.6 = 2.4$
此时你走到了$x=2.4$的位置,海拔高度是$f(2.4)=2.4^2=5.76$米—— 对比之前的9米,海拔确实下降了!第一步成功。
第四步:重复“看方向→走一步”,直到走到山谷
接下来就是“循环操作”:每次站在新位置,重新算梯度(方向)、按步长走一步,直到海拔几乎不变(到山谷了)。
我们再走几步,感受一下过程:
第2步:从$x_1=2.4$出发
- 梯度$f’(2.4)=2×2.4=4.8$(正数,继续往左边走)
- 新位置$x_2=2.4 - 0.1×4.8=2.4 - 0.48=1.92$
- 新海拔$f(1.92)=1.92^2≈3.686$米(又降了!)
第3步:从$x_2=1.92$出发
- 梯度$f’(1.92)=2×1.92=3.84$(正数,继续左走)
- 新位置$x_3=1.92 - 0.1×3.84=1.92 - 0.384=1.536$
- 新海拔$f(1.536)≈2.359$米(还在降)
第N步:慢慢靠近山谷
继续走下去,你会发现:
- $x$会从3→2.4→1.92→1.536→1.229→0.983→… 越来越接近0;
- 海拔会从9→5.76→3.686→2.359→1.510→0.966→… 越来越接近0;
- 梯度会从6→4.8→3.84→3.072→… 越来越接近0(因为$x$靠近0,$f’(x)=2x$也靠近0)。
当某一步后,比如$x$已经到0.001,下一步$x$变成0.0008,海拔从0.000001变成0.00000064—— 此时海拔几乎没变化,你就知道:“到山谷了!”(对应梯度下降的“收敛”)。
一句话总结:这个简单函数的下山过程
从$x=3$(海拔9米)出发,每次按“步长0.1”往“梯度反方向”(左走)迈一步,$x$一点点靠近0,海拔一点点降向0,最终走到$x=0$(海拔0米)—— 这就是梯度下降在简单函数上的“下山逻辑”,和线性回归里找“最好的直线”本质完全一样。
有了梯度下降这个优化算法,回归就有了“自动学习”的能力
梯度下降和正规方程的对比
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 | 不需要 |
| 需要迭代求解 | 一次运算得出 |
| 特征数量较大可以使用 | 需要计算方程,时间复杂度高 |
梯度下降法
· 全梯度下降算法(FG)
计算训练集中所有样本误差,对其求和再取平均值作为目标函数,很慢
· 随机梯度下降算法(SG)
- 每轮计算的目标函数不再是全体样本误差,而仅仅是单个样本误差,每次只代入计算一个样本目标函数的梯度来更新权重,再取下一个样本重复此过程,知道损失函数值停止下降或者损失函数值小于某个可以容忍的阈值
- 但是遇到噪声则会陷入局部最优解
· 小批量梯度下降算法(mini-bantch)
- 对上述两个方法的折中
· 随机平均梯度下降算法(SAG)
- 在SG方法中,虽然避开了运算成本过高,但对于大数据训练而言,效果不尽人意,疑问每一轮的梯度更新都与上一轮的数据和梯度无关
- 该方法在内存中为每一个样本都维护了一个旧的梯度,随机选择第i个样本来更新此样本的梯度,其他样本的梯度保持不变,然后求得所i有梯度的平均值,进而更新了参数
- 因此每一轮更新仅需计算一个样本的梯度,计算成本等同于SG,但收敛速度更快



